铁匠铺打铁视频:高中代数-数列
来源:百度文库 编辑:九乡新闻网 时间:2024/05/06 18:28:16
名称 定义 通 项 公 式 前n项的和公式 其它 数列 按照一定次序排成一列的数叫做数列,记为{an} 如果一个数列{an}的第n项an与n之间的关系可以用一个公式来表示,这个公式就叫这个数列的通项公式 等差数列 

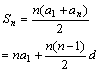
 等比数列
等比数列 
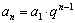

 数列前n项和与通项的关系:
数列前n项和与通项的关系:  无穷等比数列所有项的和:
无穷等比数列所有项的和:  数学归纳法 适用范围 证明步骤 注 意 事 项 只适用于证明与自然数n有关的数学命题 设P(n)是关于自然n的一个命题,如果(1)当n取第一个值n0(例如:n=1或n=2)时,命题成立(2)假设n=k时,命题成立,由此推出n=k+1时成立。那么P(n)对于一切自然数n都成立。 (1)第一步是递推的基础,第二步的推理根据,两步缺一不可
数学归纳法 适用范围 证明步骤 注 意 事 项 只适用于证明与自然数n有关的数学命题 设P(n)是关于自然n的一个命题,如果(1)当n取第一个值n0(例如:n=1或n=2)时,命题成立(2)假设n=k时,命题成立,由此推出n=k+1时成立。那么P(n)对于一切自然数n都成立。 (1)第一步是递推的基础,第二步的推理根据,两步缺一不可
(2)第二步的证明过程中必须使用归纳假设。
构造等差数列解三角题
在三角函数问题中,根据题中的信息,利用等差中项 的特征,构造相应的等差数列,可改变问题的原有结构,能沟通三角与代数的相互转化,往往会优化解题思路。
的特征,构造相应的等差数列,可改变问题的原有结构,能沟通三角与代数的相互转化,往往会优化解题思路。
一、利用两个函数的和为定值构造数列
例1. 已知 ,则
,则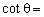 _____________________。
_____________________。
解: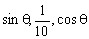
设 知
知
解得
所以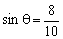 ,
,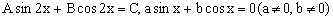 ,求证
,求证
构造数列
设 ,则
,则

所以
所以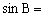 ____________________。
____________________。
解:
设
所以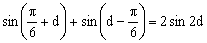
所以
所以
由 及
及 知
知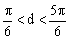
故
所以
所以

例4. 在△ABC中, ,求
,求
化简,得
由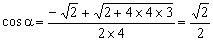
所以 的最小值。
的最小值。
解:设
构造数列
则
即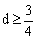
由
因为当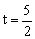 、
、
当 时,
时,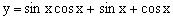 的最大值。
的最大值。
解:设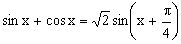
所以 ,
,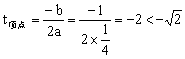
所以 为
为 最大、
最大、 、
、  、
、 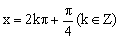

数列求和
一. 教学内容:数列求和
二. 重点、难点:
1. 公式法
2. 裂项相加
3. 裂项相消
4. 错位相减
【典型例题
[例1] 解:(1) ,< style= >
,< style= > 或1,(2)∴
或1,(2)∴
[例2] 解:迭加, 证: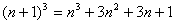
迭加
∴
∴ 另:
[例3] 解:

[例4] ,求
,求 。
。
解:
[例5] 解:∴
[例6] 若数列解:当 ∴ 当
∴ 当 ∴ 当
∴ 当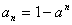
∴ 当 且
且
∴
[例7] 设正数数列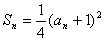 。
。
(1)求证: ,记数列解:(1)∵ ∴
,记数列解:(1)∵ ∴ ②
②
①-②得
整理得∵ ∴ ∴ 又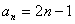
(2)∵ ∴
[例8] 求和:解:当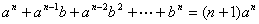
当

[例9] 数列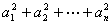 等于( )
等于( )
A. C.
C. D. 解:由得
D. 解:由得
[例10] 某渔业公司今年初用98万元购进一艘鱼船用于捕捞,第一年需要各种费用12万元,从第二年起包括维修费在内每年所需费用比上一年增加4万元,该船每年捕捞总收入50万元。问捕捞几年后总盈利最大,最大是多少?
解:设船捕捞n年后的总盈利为y万元,则


所以,当捕捞10年后总盈利最大,最大是102万元。
[例11] 一座大楼共n层,现每层指定一人步行到设在第k层的会议室开会(设每层楼梯长都相等)。问:如何确定会议室所在的楼层k,才能使n个与会人员上或下所走的楼梯总长最短?
解:设相邻两层之间的楼梯长为 ;从第k 1层、…、第n层的人所走的楼梯长依次为
;从第k 1层、…、第n层的人所走的楼梯长依次为


∵ k为整数 ∴ 当n为奇数时,k取 层;当n为偶数时,k取
层;当n为偶数时,k取 或
或 ,即会议室应设在第
,即会议室应设在第 或
或 层。
层。
【模拟试题
1. 已知数列 。若数列
。若数列 应满足的条件为( )
应满足的条件为( )
A. B.
B. C.
C.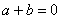 D.
D.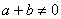
2. 在正项等比数列 ,则
,则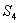 的值为( )
的值为( )
A. 28 B. 32 C. 35 D. 49
3. 等比数列 ( )
( )
A. 12 B. 10 C. 8 D.
4. 等比数列的前n项,前2n项,前3n项的和分别为A,B,C,则( )
A. A B=C B. C.
5. 在等差数列 ,A.
,A. B. 6. 等差数列A.
B. 6. 等差数列A. B.
B.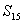 C.
C.
7. 在等差数列 是方程A. 15 B. 30 C. 50 D.
是方程A. 15 B. 30 C. 50 D.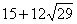
8. 在等差数列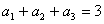 ,A. 810 B. 840 C. 870 D. 900
,A. 810 B. 840 C. 870 D. 900
9. 已知数列 ,…它的前n项的积小于A. 13 B. 14 C. 15 D. 16
,…它的前n项的积小于A. 13 B. 14 C. 15 D. 16
10. 已知数列 ,则
,则 ,直角三角形
,直角三角形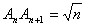 ,记
,记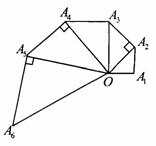
12. 正奇数集合{1,3,5,…},现在由小到大按第n组有{1} {3,5,7} {9,11,13,15,17},…
(第一组) (第二组) (第三组)
则2005位于第 组中。
13. 在等差数列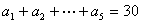 ,
, 。
。
14. 某地区荒山2200亩,从2005年开始每年春季在荒山植树造林,第一年植树100亩,以后每一年比上一年多植树50亩。(1)若所植树全部都成活,则到哪一年可将荒山全部绿化?(2)若每亩所植树苗木材量为2立方米,每年树木木材量的自然增长率为20%,那么全部绿化后的那一年年底,求该山木材总量。(精确到1立方米,参考数据: ,
, )
)

【试题答案】
1. C 2. A 3. B 4. D 5. B 6. A 7. A
8. B 9. A 10. 765 11.
12. 解:正奇数
解 得所以2005位于第32组
得所以2005位于第32组
13. 解:∵ ∴ ∴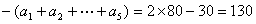
14. 解:(1)由题意可知,各年植树亩数为100,150,200,……构成等差数列
设植树n年可将荒山全部绿化,则 或
或 (舍去)
(舍去)
所以,到2012年可将荒山全部绿化
(2)2005年所植树,春季木材量为2006年所植树到2012年底木材量为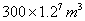 。……
。……
2012年所植树到年底木材量为 ,则到2012年底木材总量为
,则到2012年底木材总量为
上式乘以1.2,得两式相减,得所以,全部绿化后的那一年年底,该山木材总量为S=9060立方米
数列通项的计算
一. 教学内容:数列通项的计算
二. 重点、难点:
1. 直接分析法
2. 公式法
3. 由 ,求
,求

4. 由递推关系,求(1)(2)(3)
【典型例题
[例1] 写出下面数列的一个通项公式
(1)0.4,0.44,0.444,……
(2)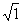 ,
, ,
, ,……
,……
(3)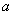 ,
,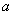 ,(4)2,3,2,1,2,3,2,1,……
,(4)2,3,2,1,2,3,2,1,……
解:(1)(2)
(3)(4)
[例2] 由 ,求(1)(2)(3)
,求(1)(2)(3)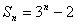

解:(1)
(2)
(3)
[例3] 。
。
解:

迭加:∴
[例4] 数列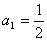 ,
, ,
, 。
。
解:


相乘

∴
∴
[例5] 数列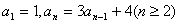 ,求解:变形∴
,求解:变形∴
∴
[例6]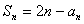 ,
, ,求解:
,求解: ∴
∴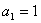

相减∴ ∴ ∴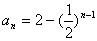
[例7] ,求解:令
,求解:令 ,
,
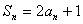

相减∴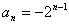
[例8] 数列 满足
满足
 。
。
解: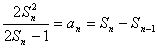
∴
∴ ∴ ∴ ∴
∴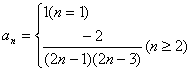
[例9] 数列 ,解:由数列
,解:由数列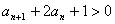
∴ ,整理为又
,整理为又 为等比数列
为等比数列
∴ 的通项公式
的通项公式
∴
[例10] 已知函数 满足(1)求数列
满足(1)求数列 是递减数列
是递减数列
解:(1)
即解得
(2)证明:

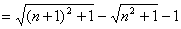

所以数列
[例11] 已知数列 的通项公式。
的通项公式。
解:当n为正偶数时,
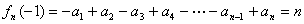
此时 为正奇数,则
为正奇数,则

∴
当n为正奇数此时 为正偶数,则
为正偶数,则
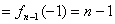
∴
而当n=1时,由已知得故数列
【模拟试题
1.
上述关于星星的图案构成一个数列,该数列的一个通项公式是( )
A.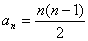
C.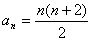
2. 设数列 ,则A. 第六项 B. 第七项 C. 第八项 D. 第九项
,则A. 第六项 B. 第七项 C. 第八项 D. 第九项
3. 数列1,0,1,0,1,……的一个通项公式为( )
A. B. C.
B. C.
4. 数列A. 107 B. 108 C. 5. 下面对数列的理解有四种:
① 数列可以看成一个定义在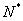 上的函数;
上的函数;
② 数列的项数是无限的;
③ 数列若用图象表示,从图象上看都是一群孤立的点;
④ 数列的通项公式是唯一的。
其中说法正确的序号是( )
A. ①②③ B. ②③④ C. ①③ D. ①②③④
6. 数列7,77,777,7777,77777,……的通项公式为 。
7. 数列 ,那么150是其第 项。
,那么150是其第 项。
8. 某细菌在培养过程中,每半小时分裂一次(一个分裂为两个),若开始只有这种细菌一个,设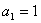 ,第一次分裂后的细菌数目为
,第一次分裂后的细菌数目为 ,第n-1次分裂后细菌数目为A.
,第n-1次分裂后细菌数目为A.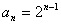 B.
B.
9. 在等比数列 是递增数列,则公比q满足( )
是递增数列,则公比q满足( )
A. D. 10. 若A. 1或2 B. 1或
D. 10. 若A. 1或2 B. 1或 C.
C.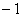 或2
或2
11. 已知等差数列 等于( )
等于( )
A. 8 B. 10 C. 12 D. 14
12.生物学中指出,生态系统中,在输入一个营养级的能量中,大约有10%?D20%的能量能够流动到下一个营养级(称为能量传递率),在H1→H2→H3→H4→H5→H6这条生物链中,若使H6获得10kJ的能量,则需要H1最多提供的能量是( )
A.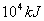 B.
B. C.
C. D.
D.
13. 数列 ,则
,则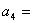 。
。
14. 在如图的表格中,每格填上一个数字后,使每一横行成等差数列,每一纵行成等比数列,则
15. 已知数列1,3,6……的各项是由一个等比数列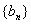 的对应项相加而得到,其中等差数列的首项为0。(1)求
的对应项相加而得到,其中等差数列的首项为0。(1)求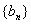 的通项公式;(2)求这个数列的前n项和
的通项公式;(2)求这个数列的前n项和 。
。
16. 已知数列 ,
, ,当
,当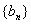
 满足
满足 。
。
(1)求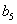 ;(2)求证:当
;(2)求证:当 。
。
17. (05年天津卷,文18)若公比为c的等比数列 (1)求c的值;(2)求数列
(1)求c的值;(2)求数列

【试题答案】
1. C 2. B 3. C 4. B 5. C
6. 7. 16 8. A 9. C
7. 16 8. A 9. C
10. D 11. C 12. C 13. 14. 1
14. 1
15. 解:(1)设数列1,3,6,…为 ,其中
,其中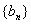 为等差数列,
为等差数列, 、数列∴
、数列∴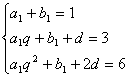
解得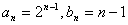
(2)
16. 解:(1)(2)证:

∴ 当(3)证:易算出当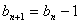 ,则
,则 为首项,公差为由
为首项,公差为由 ,解出因此,满足
,解出因此,满足 或17. 解:(1)由题设,当则
或17. 解:(1)由题设,当则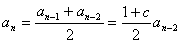
由已知条件易知 ,解得
,解得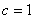 或
或
(2)当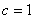 时,数列
时,数列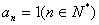 ,这时,数列当
,这时,数列当 时,数列
时,数列 的等比数列,即
的等比数列,即 的前n项和①式-①式
的前n项和①式-①式 ,得
,得



所以
等差、等比数列的综合应用
一. 教学内容:等差、等比数列的综合应用
二、教学目标:
综合运用等差、等比数列的定义式、通项公式、性质及前n项求和公式解决相关问题.
三、知识要点:
(一)等差数列
1. 等差数列的前 项和公式1:
项和公式1:
2. 等差数列的前 项和公式2:
项和公式2:
3. (m, n, p, q ∈N )
(m, n, p, q ∈N )
5. 对等差数列前n项和的最值问题有两种方法:
(1)利用 >0,d<0,前n项和有最大值,可由
>0,d<0,前n项和有最大值,可由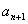 ≤0,求得n的值。
≤0,求得n的值。
当 ≤0,且
≤0,且 二次函数配方法求得最值时n的值。
二次函数配方法求得最值时n的值。
(二)等比数列
1、等比数列的前n项和公式:
∴当 ① 或
① 或 ②
②
当q=1时, 时,用公式②
时,用公式②
2、 是等比数列
是等比数列 不是等比数列
不是等比数列
②当q≠-1或k为奇数时, 仍成等比数列
仍成等比数列
3、等比数列的性质:若m n=p k,则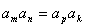
【典型例题
例1. 在等差数列{ +
+ +
+ +
+ 。
。
解:由等差中项公式: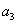 +
+ ,
, =2
=2 +
+ +
+ =450,
=450, +
+ =180
=180
 +
+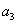 +
+ +
+ +
+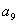
=( +
+ +
+ )+(
)+( )+=9
)+=9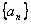 为
为 项的和。
项的和。
解:(用错项相消法)
 ①
①
①-② 时,
时,


当 时,例3. 设数列
时,例3. 设数列 项之和为
项之和为 ,若
,若 ,问:数列
,问:数列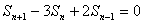 ,
,
∴
即:
 ,∴
,∴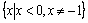 ,
,
∴即:
例4. 设首项为正数的等比数列,它的前 项之和为80,前
项之和为80,前 项中数值最大的项为54,求此数列。
项中数值最大的项为54,求此数列。
解:由题意
代入(1), ,从而
,从而
∴ 项中数值最大的项应为第
项中数值最大的项应为第 项
项
∴ ∴
∴
∴
∴此数列为
例5. 求集合M={m|m=2n-1,n∈N*,且m<60=的元素个数及这些元素的和。
 ,又∵n∈N*
,又∵n∈N*
∴满足不等式n< =
= =900
=900
答案:集合M中一共有30个元素,其和为900。
【模拟试题
1. 已知等比数列的公比是2,且前四项的和为1,那么前八项的和为 ( )
A. 15 B. 17 C. 19 D. 21
2. 已知数列{an=3n-2,在数列{an}中取ak2,akn ,… 成等比数列,若k1=2,k2=6,则k4的值 ( )
A. 86 B. 54 C. 160 D. 256
3. 数列A. 750 B. 610 C. 510 D. 505
4. <0的最小的n值是 ( )
<0的最小的n值是 ( )
A. 5 B. 6 C. 7 D. 8
5. 若一个等差数列前3项的和为34,最后3项的和为146,且所有项的和为390,
则这个数列有 ( )
A. 13项 B. 12项 C. 11项 D. 10项
6. 数列 并且
并且 。则数列的第100项为( )
。则数列的第100项为( )
A. C. 7. 在等差数列{
C. 7. 在等差数列{ =-15,公差d=3,求数列{
=-15,公差d=3,求数列{ 的元素个数,并求这些元素的和。
的元素个数,并求这些元素的和。
9. 设
(1)问数列 是否是等差数列?(2)求
是否是等差数列?(2)求 =
= +3d,∴ -15=
+3d,∴ -15= +9,
+9, =-24,
=-24,
∴ =-24n+
=-24n+ =
= [(n-
[(n- -
-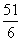 |最小时,
|最小时, 最小,
最小,
即当n=8或n=9时, =-108最小
=-108最小
解法2:由已知解得 =-24,d=3,
=-24,d=3, ≤0得n≤9且
≤0得n≤9且 =
=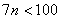 得
得 共有14个即
共有14个即 的集合
的集合
∴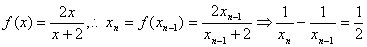
又因为
数列的基本概念与等差数列
一. 教学内容:数列的基本概念与等差数列
二. 教学目标:
1. 理解数列及其有关概念,了解数列和函数之间的关系。
2. 了解数列的通项公式,并会用通项公式写出数列的任意一项。
3. 对于比较简单的数列,会根据其前几项写出它的通项公式。
4. 明确等差数列的定义,掌握等差数列的通项公式。
5. 熟练掌握等差数列的通项公式和前n项和公式。
6. 了解等差数列的一些性质,并会用它们解决一些相关问题。
三. 本周知识要点:
4,5,6,7,8,9,10. ①
1,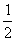 ,
, ,
, ,
,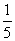 ,…. ②
,…. ②
1,0.1,0.01,0.001,0.0001,…. ③
1,1.4,1.41,1.414,…. ④
-1,1,-1,1,-1,1,…. ⑤
2,2,2,2,2,…. ⑥
观察这些例子,看它们有何共同特点?
(一)数列的基本概念
1. 数列的定义:按一定次序排列的一列数叫做数列。
2. 数列的项:数列中的每一个数都叫做这个数列的项。各项依次叫做这个数列的第1项(或首项),第2项,…,第n 项,…。
3. 数列的一般形式: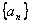 ,其中
,其中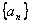 的第n项注意:⑴并不是所有数列都能写出其通项公式,如上述数列④;
的第n项注意:⑴并不是所有数列都能写出其通项公式,如上述数列④;
⑵一个数列的通项公式有时是不唯一的,如数列:1,0,1,0,1,0,…,它的通项公式可以是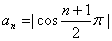
⑶数列通项公式的作用:①求数列中任意一项;②检验某数是否是该数列中的一项。
从映射、函数的观点来看,数列也可以看作是一个定义域为正整数集N*(或它的有限子集{1,2,3,…,n})的函数,当自变量从小到大依次取值时对应的一列函数值,数列的通项公式就是相应函数的解析式。
对于函数,我们可以根据其函数解析式画出其对应图象,看来,数列也可根据其通项公式画出其对应图象,下面同学们练习画数列①,②的图象,并总结其特点。

5. 数列的图像都是一群孤立的点。
6. 数列有三种表示形式:列举法,通项公式法和图象法。
7. 有穷数列:项数有限的数列。例如,数列①是有穷数列。
8. 无穷数列:项数无限的数列。
(二)等差数列
1. 等差数列:一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,这个数列就叫做等差数列,这个常数就叫做等差数列的公差(常用字母“d”表示)。
⑴公差d一定是由后项减前项所得,而不能用前项减后项来求;
⑵对于数列{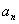 -
-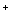 ,则此数列是等差数列,d 为公差。
,则此数列是等差数列,d 为公差。
2. 等差数列的通项公式:
3. 等差中项:如果a,A,b成等差数列,那么A叫做 a与b的等差中项。
如数列:1,3,5,7,9,11,13…中
5是3和7的等差中项,1和9的等差中项。
9是7和11的等差中项,5和13的等差中项。
看来,4. 性质:在等差数列中,若m n=p q,则, (m, n, p, q ∈N )
(m, n, p, q ∈N )
但通常 ①由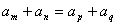 推不出m n=p q ,②
推不出m n=p q ,②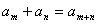
5. 等差数列的前 项和公式 (1)
项和公式 (1) (2)
(2)
公式二又可化成式子:若 。
。
【典型例题
例1. 根据下面数列
解:(1)
例2. 写出下面数列的一个通项公式,使它的前4项分别是下列各数:
(1)1,3,5,7;
(2) ,-
,- .
.
解:
(1)项1=2×1-1 3=2×2-1 5=2×3-1 7=2×4-1
↓ ↓ ↓ ↓
序号 1 2 3 4
即这个数列的前4项都是序号的2倍减去1,
∴它的一个通项公式是: (2)序号:1 2 3 4
↓ ↓ ↓ ↓
项分母:2=1 1 3=2 1 4=3 1 5=4 1
↓ ↓ ↓ ↓
项分子: 22-1 32-1 42-1 52-1
即这个数列的前4项的分母都是序号加上1,分子都是分母的平方减去1,∴它的一个通项公式是:
这个数列的前4项的绝对值都等于序号与序号加1的积的倒数,且奇数项为负,偶数项为正,所以它的一个通项公式是: 例3. ⑴求等差数列8,5,2…的第20项
⑵ -401是不是等差数列-5,-9,-13…的项?如果是,是第几项?

n=20,得⑵由得数列通项公式为: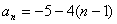
由题意可知,本题是要回答是否存在正整数n,使得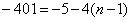 成立解之得n=100,即-401是这个数列的第100项。
成立解之得n=100,即-401是这个数列的第100项。
例4. 在等差数列 ,求
,求 ,
, ,
,
解法一:∵ ,
,
 ∴解法二:∵ ∴
∴解法二:∵ ∴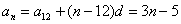
小结:第二通项公式 【模拟试题】
1、根据下面数列的前几项的值,写出数列的一个通项公式:
(1)3, 5, 9, 17, 33,……;
(2) ,
,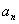 }中,(1)已知
}中,(1)已知 =19,求
=19,求 与d;(2)已知
与d;(2)已知 =3,求
=3,求 。
。
4、在等差数列 ,
,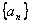 中, 若
中, 若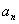 =2n+1;
=2n+1;
(2)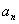 =
= ;
;
(4)将数列变形为1+0, 2+1, 3+0, 4+1, 5+0, 6+1, 7+0, 8+1, ……,
∴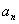 =(-1)
=(-1) n(n+1)
n(n+1)
2、(1)解:根据题意可知: =3,d=7-3=4
=3,d=7-3=4
∴该数列的通项公式为: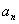 =4n-1(n≥1,n∈N*)
=4n-1(n≥1,n∈N*)
∴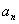 =10 (n-1)×(-2),即:<1" style='width:14.25pt; >
=10 (n-1)×(-2),即:<1" style='width:14.25pt; >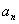 =-2n 12,
=-2n 12,
∴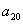 =-2×20 12=-28.
=-2×20 12=-28.
(3)解:根据题意可得:<3" > =2,d=9-2=7.
=2,d=9-2=7.
∴此数列通项公式为: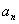 =-<8" >
=-<8" >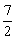 n <9" >
n <9" >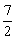 ,
,
令-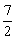 n
n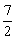 =-20,解得n=
=-20,解得n=
因为-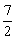 n
n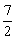 =-20没有正整数解,所以-20不是这个数列的项。
=-20没有正整数解,所以-20不是这个数列的项。
3、解:(1)由题意得: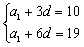 解之得:
解之得:
(2)解法一:由题意可得: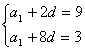 , 解之得
, 解之得
∴该数列的通项公式为: =
= 3d,∴
3d,∴ =3 3×(-1)=0.
=3 3×(-1)=0.
4、解:由题意可知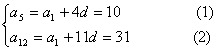
解之得 ,即这个数列的首项是-2,公差是3。
,即这个数列的首项是-2,公差是3。
或由题意可得: ,即:31=10 7d
,即:31=10 7d
可求得d=3,再由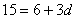
数列、等差数列
一. 教学内容:
2.1 数列
2.2 等差数列
二. 教学目的:
1. 了解数列的概念,体会数列是一种特殊函数,能根据数列的前几项写出简单数列的通项公式。
2. 类比函数理解数列的几种表示方法(列表、图象、通项公式等),能根据项数多少、数列的性质对数列分类。
3. 掌握等差数列的概念、等差中项的概念,会根据定义判定数列是否是等差数列。
4. 掌握等差数列的通项公式及推导方法,会类比直线、一次函数等有关知识研究等差数列的性质,能熟练运用通项公式求有关的量:a1,d,n,an。
5. 掌握等差数列的前n项和公式及推导方法.当al,d,n,an,Sn中已知三个量时,能熟练运用通项公式、前n项和公式求另两个量。灵活运用公式解决与等差数列有关的综合问题。能构建等差数列模型解决实际问题。
三. 教学重点、难点:
重点:数列的概念、数列的通项公式;等差数列的通项公式和前n项和公式。
难点:等差数列的通项公式和前n项和公式的推导以及它们的综合运用。
四. 知识分析:
(一)数列
1. 数列的定义:按照一定次序排列的一列数叫数列,数列中每一个数叫这个数列的项,第n项记作an,叫做数列的通项,我们常把一般形式的数列简记作{an}。
2. 数列是特殊函数
数列可以看成以正整数集N+(或它的有限子集{1,2,3,…,n})为定义域的函数。an=f(n),当自变量按照从小到大依次取值时,所对应的一列函数值。
3. 通项公式:如果数列{an}的第n项与项数n之间的函数关系,可以用一个公式an=f(n)来表示,那么就把这个公式叫这个数列的通项公式。
通项公式可以看成数列的函数解析式。
4. 数列的分类:
(1)按项数有限还是无限来分:有穷数列和无穷数列;
(2)按照项与项之间的大小关系来分:递增数列、递减数列、摆动数列、常数列。
5. 前面学习过数集,如果把数集中的元素按一定顺序排成一列,就是数列。但数列和数集有较大区别:数集中的元素是无序的,也是互异的;而数列中的元素却是有序的,而且是可以重复出现的。
6. 根据所给出的数列的前几项,写出符合要求的一个通项公式,主要方法是:
①要观察给出的若干数中的“不变”的内容,注意研究an与n的关系。
②多角度思考,全方位观察,广泛联想,将原数列作出适当的转化变形后,化为基本数列或特殊数列,常用技巧是:分解条件,寻找规律。
7. 如何利用数列与函数的关系来解题?
一方面,数列是一个特殊的函数,因此在解决数列问题时,要善于利用函数的知识、函数的观点、函数的思想方法来解题,即用共性来解决特殊问题。如由数列是定义在N*和它的子集{1,2,3,…,n}的函数可知an是n的函数,即an=f(n)。因此当{an}通项公式的一端的某个“n”用某个数或某个式或某个记号代替后,则两端的所有的“n”必须用同一个代替,特别地有 ),则图象呈上升趋势,即数列是递增的,即an递增
),则图象呈上升趋势,即数列是递增的,即an递增 ,对任意的n(n∈N*)都成立。类似地有{an}递减< >
,对任意的n(n∈N*)都成立。类似地有{an}递减< >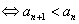 。对任意的n(n∈N*)都成立。
。对任意的n(n∈N*)都成立。
8. 如果已知数列{an}的第一项(或前几项),且从第二项(或某一项)开始的任一项an与它的前一项an-1(或前几项)间的关系可以用一个式子来表示,那么这个公式叫做这个数列的递推公式。
9. 若数列{an}的前n项和记为Sn,即 ,则
,则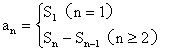 。
。
10. 通项公式和递推公式的区别在于:通项公式直接反映an和n之间的关系,即an是n的函数,知道任意一个具体的n值,通过通项公式就可以求出该项的值an;而递推公式则是间接反映数列的式子,它是数列任意两个(或多个)相邻项之间的推导关系,不能由n直接得出an
11. 用递推公式给出一个数列,必须给出①“基础”?D?D数列{an}的第1项或前几项;②递推关系?D?D数列{an}的任一项an与它的前一项an-1(或前几项)之间的关系,并且这个关系可以用一个公式来表示。
如果两个条件缺一个,数列就不能确定。例如,已知数列{an}的al=1,a2=2,这个数列就不能确定。因为有的说an=n;有的说 ,则
,则 ,将这些等式相加得到
,将这些等式相加得到
若a1适合 ,则用一个公式表示an,若al不适合
,则用一个公式表示an,若al不适合 ,则要用分段形式表示an,此处切不可不求a1,而直接求an.
,则要用分段形式表示an,此处切不可不求a1,而直接求an.
(二)等差数列
1. 等差数列的定义:一般地,如果一个数列{an}从第二项起,每一项与它的前一项的差都等于同一个常数,用式子可表示为 ,则数列{an}叫做等差数列。常数d叫做等差数列的公差。
,则数列{an}叫做等差数列。常数d叫做等差数列的公差。
2. 等差数列的单调性:等差数列的公差d>0时,数列为递增数列;d<0时,数列为递减数列;d=0时,数列为常数列。
3. 等差数列的通项公式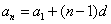
4. 要证明数列{an}为等差数列,只要证明:当 等于同一个常数d。
等于同一个常数d。
5. 对等差数列{an}而言:
(l)公差是从第二项起,每一项减去它前一项的差(同一常数),即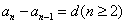 都成立。
都成立。
(3) 时,an是关于n的一次函数。故
时,an是关于n的一次函数。故 的图象是直线y=dx (a1?Dd)上当x∈N*时的点的集合。
的图象是直线y=dx (a1?Dd)上当x∈N*时的点的集合。
由此可利用共线的方法解决有关等差数列问题。
(4)对任意的m,n∈N*,有 。
。
(5)公式中含四个量a1,an,d,n,已知任意三个,可求第四个量。
6. 如果三个数a,A,b组成等差数列,那么A叫做a与b的等差中项。
7. 等差数列的判定方法
(1) 。
。
(3) 。
。
(5)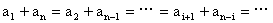 。
。
(7)数列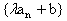 (
( 、b是常数)是公差为
、b是常数)是公差为 的等差数列。
的等差数列。
(8)下标成等差数列且公差为m的项 组成公差为md的等差数列。
组成公差为md的等差数列。
(9)若 也为等差数列,则
也为等差数列,则 仍成等差数列(首项不一定选
仍成等差数列(首项不一定选 )。
)。
(11) 是等差数列,则
是等差数列,则 。
。
(2)若有三个数成等差数列,则一般设为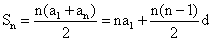
2. 若数列{an}的前n项和公式为 可进一步变形为:
可进一步变形为:
 ,若令
,若令 ,
,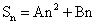 (*),(*)式是等差数列前n项和公式的另一种表达形式。
(*),(*)式是等差数列前n项和公式的另一种表达形式。
(2)当A≠0,即d≠0时,(*)式是n的二次函数,即(n,Sn)在 的图象上,因此,当d≠0时,数列S1,S2,S3,…,Sn的图象是抛物线
的图象上,因此,当d≠0时,数列S1,S2,S3,…,Sn的图象是抛物线 上的一群离散的点。
上的一群离散的点。
(3)在求等差数列的和Sn时,如已知al、an、n,可用公式 来解,如已知al、n、d,则可用公式
来解,如已知al、n、d,则可用公式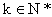 )是等差数列,其公差等于kd。
)是等差数列,其公差等于kd。
6 . 若在等差数列{an}中,a1>0,d<0,则Sn存在最大值;若在等差数列{an}中,a1<0,d>0,则Sn存在最小值。
7. 若
(四)与和有关的等差数列的性质:
1. 若项数为2n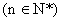 ,则
,则 ;
;
若项数为 ,
,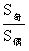
 。
。
4. 若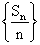 也为等差数列。
也为等差数列。
【典型例题】
例1. 写出下面数列的一个通项公式,使它的前4项分别是下列各数:
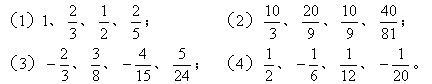
解析:若要根据给出的前 4 项写出数列的通项公式,首先要细心观察四个数变化的规律,为了便于发现规律应注意两点:
第一是将个别破坏规律的项还原,如(l)中首先观察发现第一个数1应写成分数 ,然后发现分母应从小变大,则第三个数应还原为
,然后发现分母应从小变大,则第三个数应还原为 。再由
。再由 很容易写出其通项公式。(2)题中由分母为31、32、33、34,分子为10、20、10、40,发现均为第三个数破坏了规律,分析可知应还原为
很容易写出其通项公式。(2)题中由分母为31、32、33、34,分子为10、20、10、40,发现均为第三个数破坏了规律,分析可知应还原为 ,再写分子为n 1,最后写分母为
,再写分子为n 1,最后写分母为 ,又如(4)的分母的规律不易看出,可将分母一分为二,变为
,又如(4)的分母的规律不易看出,可将分母一分为二,变为 ,
,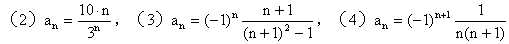 。
。
点评:
1. 求数列的通项公式时,一般通过分解?D?D探索?D?D综合的方法进行归纳。要注意观察数列中的各项通过分解后哪些部分是不变的,哪些部分是变化的,变化的部分随其序号的变化情况如何,归纳时要重视从整体上把握数列的构成规律,写出通项公式。
2. 为了方便,掌握下面一些简单的常用数列的通项公式是有好处的:



 。求证:当
。求证:当
 。
。
证明: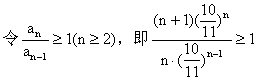

整理得 解得n≥9
解得n≥9
∴从第1项到第9项递增,从第10项起递减。
点评:数列是特殊函数,可用研究函数的方法研究数列相应问题(如本题数列的增减性)
例3. 已知数列 为等差数列,
为等差数列, 。
。
解法一:设数列 的首项为
的首项为 ,公差为d
,公差为d
由已知得360docimg_501_
解之得360docimg_502_
360docimg_503_
360docimg_504_
则由题设,得360docimg_505_
故所求四数分别为2,5,8,11或11,8,5,2
解法二:设这四个数分别为360docimg_506_
360docimg_507_
所以所求四数分别为2,5,8,11或11,8,5,2
点评:本题巧设未知数,减少了未知量,简化了运算。一般地,三个数成等差数列,且它们的和已知时,可设为a-d,a,a d。而四个数可设为a-3d,a-d,a d,a 3d(公差为2d)。
例5. (2005年北京市模拟题)已知a,b,c成等差数列,那么a2(b+c),b2(c a),c2(a b)是否构成等差数列?
证明:∵a,b,c成等差数列 ∴360docimg_508_
360docimg_509_
即360docimg_510_。
(2)360docimg_511_
整理得360docimg_512_
解之得n=12或360docimg_513_
解之得n=4
又由360docimg_514_
即得360docimg_515_
360docimg_516_
360docimg_517_
解法二:由360docimg_518_
得360docimg_519_
360docimg_520_
点评:a1,d,n称为等差数列的三个基本量,an和Sn都可以用这三个基本量来表示,五个量 a1,d,n,an,Sn中可知三求二,即等差数列的通项公式及前n项和公式中“知三求二”的问题,一般是通过通项公式和前n项和公式联立方程(组)求解。这种方法是解决数列运算的基本方法,在具体求解过程中应注意已知与未知的联系及整体思想的运用。
例7. 已知数列360docimg_521_的前n项和360docimg_522_,求数列360docimg_523_的前n项和360docimg_524_
∵n=1也适合上式
∴数列360docimg_525_
由360docimg_526_时
360docimg_527_
(2)当360docimg_528_
故360docimg_529_
点评:由an与Sn的关系求通项公式是一类重要题型,要注意分类讨论的必要性。
例8. (2005年西安市统考题)一个等差数列的前10项之和为100,前100项之和为10,求前110项之和。
解法一:设等差数列360docimg_530_的公差为d,前n项和360docimg_531_
则360docimg_532_
由已知得360docimg_533_
①×10-②整理得360docimg_534_
360docimg_535_
360docimg_536_
故此数列的前110项之和为-110
解法二:设360docimg_537_
360docimg_538_
360docimg_539_
解法三:设等差数列的首项为360docimg_540_,公差为d
则360docimg_541_
①-②得
360docimg_542_
360docimg_543_成等差数列,设其公差为D。前10项的和360docimg_544_
360docimg_545_
又360docimg_546_
点评:本例解法较多,望同学们认真分析每种解法的思想实质,达到开阔思想探索研究,寻求简捷解法的目的。解法一是基本方法,不容忽视,解法二属函数观点,高瞻远瞩,解法三运用整体思想,解法四则利用性质,简捷明快,解法五利用了等差数列的性质。
【模拟试题】
1. 数列360docimg_547_的通项公式360docimg_548_,作为函数,它的定义域是( )
A. 正整数集N*
B. 自然数集N
C. 正整数集N*或N*的任一子集
D. 正整数集N*,或其有限子集{1,2,…,n}
2. 下列说法中,正确的是( )
A. 数列1,3,5,7可表示为{1,3,5,7}
B. 数列1,0,-1,-2与数列-2,-1,0,1是相同的数列
C. 数列360docimg_549_)两数之间插入n个数,使它们与a,b组成等差数列,则该数列的公差为( )
A.360docimg_550_C.360docimg_551_
4. 在数列{360docimg_552_,则360docimg_553_都是等差数列,且360docimg_554_,则360docimg_555_+360docimg_556_,则此数列前20项的和等于( )
A. 160 B. 180 C. 200 D. 220
7. (2004年福建文)设Sn是等差数列360docimg_557_的前n项和,若360docimg_558_( )
A. 1 B. -1 C. 2 D.360docimg_559_
8. (2004年重庆卷)若360docimg_560_是等差数列,首项360docimg_561_成立的最大自然数n是( )
A. 4005 B. 4006 C. 4007 D. 4008
9. (2005年吉林省实验中学第一次检测)在等差数列360docimg_562_中,360docimg_563_,则360docimg_564_等于__________。
11. 等差数列360docimg_565___________。
12. 在数列360docimg_566_中,已知360docimg_567_,那么使其前n项和360docimg_568_,两个数列:360docimg_569_都是等差数列,求360docimg_570_
其中每行、每列都是等差数列,360docimg_571_的计算公式。
15. 设360docimg_572_为等差数列,360docimg_573_为数列360docimg_574_的前n项和,已知360docimg_575_的前n项和,求360docimg_576_。
(1)求通项360docimg_577_12. 12
13. 解:设两个等差数列的公差分别为360docimg_578_
解得360docimg_579_
14. 解:(1)360docimg_580_
第二行是首项为7,公差为5的等差数列
360docimg_581_,公差为360docimg_582_
15. 解:设等差数列360docimg_583_的公差为d,则
360docimg_584_
解得360docimg_585_
360docimg_586_
360docimg_587_
360docimg_588_
16. 解:(1)360docimg_589_
360docimg_590_
360docimg_591_
360docimg_592_
360docimg_593_
故360docimg_594_
数列通项与数列求和
一. 教学内容:数列通项与数列求和
二. 教学要求:
n求an时,用公式an=Sn-1要注意a1应由an+1-f(n),f(an+1=q,分别用累加法、累乘法、迭代法(或换元法).
2、数列的前n项和
(1)数列求和的常用方法有:公式法、分组求和法、错位相减法、裂项相消法、倒序求和法等。
求数列的前n项和,一般有下列几种方法:
(2)等差数列的前n= = .
(3)等比数列的前q=1时,Sq≠1时,Sn的数列,求前n项和时,应注意讨论n的奇偶性。
③倒序相加和错位相减法是课本中分别推导等差、等比数列前360docimg_595_,360docimg_596_是等比数列,并求360docimg_597_,∴360docimg_598_
假设存在某个360docimg_599_,则可以推出与360docimg_600_矛盾。
∴360docimg_601_。
例2. 在数列360docimg_602_=n?360docimg_603_的表达式。
360docimg_604_的前n项和Sn的公式,求360docimg_605_
例4. 设数列解:设360docimg_606_
例5. (天津文20)在数列360docimg_607_中,360docimg_608_,360docimg_609_.
(I)证明数列360docimg_610_是等比数列;
(II)求数列360docimg_611_的前360docimg_612_项和360docimg_613_,得
360docimg_614_.
又360docimg_615_是首项为360docimg_616_,且公比为360docimg_617_,于是数列360docimg_618_的通项公式为
360docimg_619_.
所以数列360docimg_620_的前360docimg_621_项和360docimg_622_.
例6. 已知数列:1,360docimg_623_,360docimg_624_,求它的前n项的和Sn.
解:∵360docimg_625_+360docimg_626_+……+360docimg_627_
=360docimg_628_∴an=2-360docimg_629_
则原数列可以表示为:
(2-1),360docimg_630_,360docimg_631_,…前n=(2-1)+360docimg_632_+…+=2360docimg_633_
=2360docimg_634_=2n-2=360docimg_635_+2n-2
例7. 已知数列{n项和Sn2-9(1)求证:{ n的最小值及相应的n项和为Tn,求T解:(1)a1=S1=-8
an=Sn-1=2
∴ n-10 an=2
∴ {n=n2-9n-360docimg_636_)2-360docimg_637_
∴当n=4或n有最小值-20.
(3)n-10 ∴ | an |=| 2an≥0360docimg_638_n≤4时,|n
Tn=360docimg_639_,当n=-a2-a4+a6+…+=(a1+a2+…+an)-(a1+a2+a3+a4)=S=n2-9n2-9n=360docimg_640_
数列360docimg_641_项和。
360docimg_642_,求前360docimg_643_项和。
360docimg_644_
360docimg_645_
例11. 已知函数f(x)=(x-1)2,数列{an}是公差为d的等差数列,数列{bn}是公比为q的等比数列(q≠1),若a1=f(d-1),a3=f(d+1),b1=f(q-1),b3=f(q+1),
(1)求数列{an},{bn}的通项公式;
(2)设数列{cn}对任意的自然数n均有:360docimg_646_,求数列{cn}的前n项和Sn.
解:(1) d-2)2,d2,a3-a1=2d2-(d-2)2=2d,解之得a1=0,n-1)
又b1=(q-2)2,q2,b3=b1q2
即q2=(q-2)2q=3
∴b1=1,n-1
(2)360docimg_647_
n
=4(1×30+2×31+3×32+…+ n-1)
设n×3360docimg_648_1×31+2×32+3×33+…+n×3360docimg_649_1+3+32+33+…+3n×3360docimg_650_n?n
360docimg_651_
∴Sn=2n?3n+1
【模拟试题
1. 数列360docimg_652_=
3. 数列{360docimg_653_的前20项和为
4. 已知数列360docimg_654_的通项公式为
5. 设360docimg_655_则360docimg_656_的值为
6. 求数列1,360docimg_657_的前360docimg_658_项和。
7. 数列360docimg_659_的前360docimg_660_项和360docimg_661_项和360docimg_662____________
9. 数列360docimg_663_的前360docimg_664_项和为
10. 求和:360docimg_665_项和的公式的方法,可求得
360docimg_666_360docimg_667_,360docimg_668_,求:13. 已知数列{an}是公差为d的等差数列,数列{bn}是公比为q(q∈R且q≠1)的等比数列,若函数f (x)=(x-1)2,且a1 = f (d-1),a3 = f (d 1),b1 = f (q 1),b3 = f (q-1),求数列{ a n }和{ b n }的通项公式。
360docimg_669_
【试题答案】
1.360docimg_670_,
360docimg_671_
7.360docimg_672_
8. 1
9.360docimg_673_
10.
360docimg_674_
11.360docimg_675_
360docimg_676_
360docimg_677_
等比数列、数列求和
一. 教学内容:等比数列、数列求和
二. 重点、难点:
1. 理解等比数列的有关概念;掌握等比数列的通项公式和前360docimg_678_项和公式,并能运用这些知识解决一些简单的实际问题。
2. 通过观察数列通项公式的特点选择合适的方法,求数列的前360docimg_679_项和。
【典型例题
[例1] 在等比数列360docimg_680_,360docimg_681_,求360docimg_682_和360docimg_683_是等比数列,故360docimg_684_,结合360docimg_685_,可知360docimg_686_的两根,解方程,得360docimg_687_
故360docimg_688_,360docimg_689_或360docimg_690_时,360docimg_691_,得360docimg_692_,故360docimg_693_360docimg_694_
当360docimg_695_时,360docimg_696_
综上所述,360docimg_697_或360docimg_698_
[例2] 已知数列360docimg_699_,360docimg_700_,360docimg_701_
解:设360docimg_702_成等比数列
∴360docimg_703_
∵360docimg_704_
∴360docimg_705_
360docimg_706_为等差数列,360docimg_707_,360docimg_708_。
解:由360docimg_709_为等比数列
∴360docimg_710_
由已知360docimg_711_∵360docimg_712_∴360docimg_713_知360docimg_714_
360docimg_715_知
360docimg_716_或360docimg_717_或360docimg_718_
[例4] 设等比数列360docimg_719_,360docimg_720_)
解:方法一:设公比为360docimg_721_化简得360docimg_722_解得360docimg_723_
设数列360docimg_724_前360docimg_725_项和为360docimg_726_,则
360docimg_727_360docimg_728_360docimg_729_
可见,当360docimg_730_时,<4" >360docimg_731_最大
而360docimg_732_,
故360docimg_733_的前5项和最大
方法二:接前,360docimg_734_于是360docimg_735_
∴ 数列<9" >360docimg_736_是以360docimg_737_为首项,以360docimg_738_,得360docimg_739_
由于360docimg_740_∴360docimg_741_的前5项和最大
[例5] 求数列的前360docimg_742_项和:360docimg_743_
360docimg_744_时,360docimg_745_时,
360docimg_746_
[例6] 在数列360docimg_747_,求数列360docimg_748_项的和。
解:∵360docimg_749_
∴ 数列360docimg_750_项和
360docimg_751_
360docimg_752_的值。
解:设360docimg_753_①
将①式右边反序得
360docimg_754_
① ②得360docimg_755_
[例8] 已知数列360docimg_756_的表达式;
(2)如果360docimg_757_,求360docimg_758_项和360docimg_759_
解:
(1)360docimg_760_,当360docimg_761_
∴360docimg_762_
因而360docimg_763_
∴360docimg_764_①
则360docimg_765_360docimg_766_
360docimg_767_又1 3 5 …360docimg_768_
[例9] 已知数列360docimg_769_项和为360docimg_770_,且满足360docimg_771_),360docimg_772_是等差数列;
(2)求360docimg_773_时,求证:360docimg_774_
解:
(1)证明:∵360docimg_775_
360docimg_776_
又360docimg_777_∴360docimg_778_
∴ 当360docimg_779_[或360docimg_780_]
当360docimg_781_时,360docimg_782_
∴360docimg_783_
(3)证明:由(2)知,
360docimg_784_
360docimg_785_中,首项360docimg_786_等于( )
A. 33 B. 72 C. 84 D. 189
2. 若等比数列360docimg_787_的公比360docimg_788_项和为360docimg_789_,则360docimg_790_与360docimg_791_的大小关系是( )
A.360docimg_792_C.360docimg_793_满足360docimg_794_(360docimg_795_),则当360docimg_796_时,360docimg_797_B.360docimg_798_C.360docimg_799_中,若360docimg_800_B.360docimg_801_D.360docimg_802_(360docimg_803_)的结果是( )
A.360docimg_804_C.360docimg_805_D.360docimg_806_
6. 数列360docimg_807_项和为360docimg_808_,则360docimg_809_等于( )
A. 1003 B.360docimg_810_C. 2006 D.360docimg_811_等于( )
A.360docimg_812_
B.360docimg_813_
D.360docimg_814_,第三年的增长率为360docimg_815_,则下列关系正确的是( )
A.360docimg_816_C.360docimg_817_
二. 解答题:
1. 等比数列360docimg_818_项中,数值最大的一项是54,若该数列的前360docimg_819_,求:
(1)前100项之和360docimg_820_。
2. 已知数列1,360docimg_821_,360docimg_822_(360docimg_823_项和。
3. 已知360docimg_824_
(1)当360docimg_825_的前360docimg_826_项和360docimg_827_;
(2)求360docimg_828_
4. 设数列360docimg_829_的等差数列,求和:360docimg_830_
360docimg_831_
360docimg_832_
【试题答案】
一.
1. C
解析:∵360docimg_833_,360docimg_834_或2. A
解析:由等比数列通项公式和前360docimg_835_项和公式得
360docimg_836_
360docimg_837_
360docimg_838_又360docimg_839_, 即3. C
解析:由已知360docimg_840_
得到360docimg_841_,360docimg_842_由此猜想出4. D
解析:由360docimg_843_),当360docimg_844_时,360docimg_845_不适合,所以360docimg_846_
5. B
解析:∵360docimg_847_
360docimg_848_
6. A
解析:360docimg_849_(共1003个)=1003
7. D
解析:原式360docimg_850_
8. B
解析:设平均增长率为360docimg_851_,则第三年产量为360docimg_852_,所以应该有360docimg_853_
即360docimg_854_
二.
1. 解:设公比为360docimg_855_
∴360docimg_856_(∵360docimg_857_②
360docimg_858_③
由①②③解得360docimg_859_,则
(1)前100项之和360docimg_860_
(2)通项公式为360docimg_861_
2. 解:由题意可知,360docimg_862_的通项是等差数列360docimg_863_的通项与等比数列360docimg_864_的通项之积,设①-②得当360docimg_865_
∴360docimg_866_
当360docimg_867_时,360docimg_868_
3. 解析:
(1)当360docimg_869_,这时数列360docimg_870_项和360docimg_871_①
①式两边同乘以360docimg_872_,得360docimg_873_
若360docimg_874_
360docimg_875_
若360docimg_876_时,360docimg_877_
则360docimg_878_
当360docimg_879_
360docimg_880_此时,360docimg_881_
若360docimg_882_,360docimg_883_
若360docimg_884_,360docimg_885_
4. 解析:∵ ∴ ∴ 又360docimg_886_
(2)第二步的证明过程中必须使用归纳假设。
构造等差数列解三角题
在三角函数问题中,根据题中的信息,利用等差中项
一、利用两个函数的和为定值构造数列
例1. 已知
解:
设
解得
所以
构造数列
设
所以
所以
解:
设
所以
所以
所以
由
故
所以
所以
例4. 在△ABC中,
化简,得
由
所以
解:设
构造数列
则
即
由
因为当
当
解:设
所以
所以
数列求和
一. 教学内容:数列求和
二. 重点、难点:
1. 公式法
2. 裂项相加
3. 裂项相消
4. 错位相减
【典型例题
[例1] 解:(1)
[例2] 解:迭加, 证:
迭加
∴
∴ 另:
[例3] 解:
[例4]
解:
[例5] 解:∴
[例6] 若数列解:当
∴ 当
∴
[例7] 设正数数列
(1)求证:
①-②得
整理得∵ ∴ ∴ 又
(2)∵ ∴
[例8] 求和:解:当
当
[例9] 数列
A.
[例10] 某渔业公司今年初用98万元购进一艘鱼船用于捕捞,第一年需要各种费用12万元,从第二年起包括维修费在内每年所需费用比上一年增加4万元,该船每年捕捞总收入50万元。问捕捞几年后总盈利最大,最大是多少?
解:设船捕捞n年后的总盈利为y万元,则
所以,当捕捞10年后总盈利最大,最大是102万元。
[例11] 一座大楼共n层,现每层指定一人步行到设在第k层的会议室开会(设每层楼梯长都相等)。问:如何确定会议室所在的楼层k,才能使n个与会人员上或下所走的楼梯总长最短?
解:设相邻两层之间的楼梯长为
∵ k为整数 ∴ 当n为奇数时,k取
【模拟试题
1. 已知数列
A.
2. 在正项等比数列
A. 28 B. 32 C. 35 D. 49
3. 等比数列
A. 12 B. 10 C. 8 D.
4. 等比数列的前n项,前2n项,前3n项的和分别为A,B,C,则( )
A. A B=C B. C.
5. 在等差数列
7. 在等差数列
8. 在等差数列
9. 已知数列
10. 已知数列
12. 正奇数集合{1,3,5,…},现在由小到大按第n组有{1} {3,5,7} {9,11,13,15,17},…
(第一组) (第二组) (第三组)
则2005位于第 组中。
13. 在等差数列
14. 某地区荒山2200亩,从2005年开始每年春季在荒山植树造林,第一年植树100亩,以后每一年比上一年多植树50亩。(1)若所植树全部都成活,则到哪一年可将荒山全部绿化?(2)若每亩所植树苗木材量为2立方米,每年树木木材量的自然增长率为20%,那么全部绿化后的那一年年底,求该山木材总量。(精确到1立方米,参考数据:
【试题答案】
1. C 2. A 3. B 4. D 5. B 6. A 7. A
8. B 9. A 10. 765 11.
12. 解:正奇数
解
13. 解:∵ ∴ ∴
14. 解:(1)由题意可知,各年植树亩数为100,150,200,……构成等差数列
设植树n年可将荒山全部绿化,则
所以,到2012年可将荒山全部绿化
(2)2005年所植树,春季木材量为2006年所植树到2012年底木材量为
2012年所植树到年底木材量为
上式乘以1.2,得两式相减,得所以,全部绿化后的那一年年底,该山木材总量为S=9060立方米
数列通项的计算
一. 教学内容:数列通项的计算
二. 重点、难点:
1. 直接分析法
2. 公式法
3. 由
4. 由递推关系,求(1)(2)(3)
【典型例题
[例1] 写出下面数列的一个通项公式
(1)0.4,0.44,0.444,……
(2)
(3)
解:(1)(2)
(3)(4)
[例2] 由
解:(1)
(2)
(3)
[例3]
解:
迭加:∴

[例4] 数列
解:
相乘
∴
∴
[例5] 数列
∴
[例6]
相减∴ ∴ ∴
[例7]
相减∴
[例8] 数列
解:
∴
∴ ∴ ∴ ∴
∴
[例9] 数列
∴
∴
∴
[例10] 已知函数
解:(1)
即解得
(2)证明:
所以数列
[例11] 已知数列
解:当n为正偶数时,
此时
∴
当n为正奇数此时
∴
而当n=1时,由已知得故数列
【模拟试题
1.
上述关于星星的图案构成一个数列,该数列的一个通项公式是( )
A.
C.
2. 设数列
3. 数列1,0,1,0,1,……的一个通项公式为( )
A.
4. 数列A. 107 B. 108 C. 5. 下面对数列的理解有四种:
① 数列可以看成一个定义在
② 数列的项数是无限的;
③ 数列若用图象表示,从图象上看都是一群孤立的点;
④ 数列的通项公式是唯一的。
其中说法正确的序号是( )
A. ①②③ B. ②③④ C. ①③ D. ①②③④
6. 数列7,77,777,7777,77777,……的通项公式为 。
7. 数列
8. 某细菌在培养过程中,每半小时分裂一次(一个分裂为两个),若开始只有这种细菌一个,设
9. 在等比数列
A.
11. 已知等差数列
A. 8 B. 10 C. 12 D. 14
12.生物学中指出,生态系统中,在输入一个营养级的能量中,大约有10%?D20%的能量能够流动到下一个营养级(称为能量传递率),在H1→H2→H3→H4→H5→H6这条生物链中,若使H6获得10kJ的能量,则需要H1最多提供的能量是( )
A.
13. 数列
14. 在如图的表格中,每格填上一个数字后,使每一横行成等差数列,每一纵行成等比数列,则
15. 已知数列1,3,6……的各项是由一个等比数列
16. 已知数列
(1)求
17. (05年天津卷,文18)若公比为c的等比数列
【试题答案】
1. C 2. B 3. C 4. B 5. C
6.
10. D 11. C 12. C 13.
15. 解:(1)设数列1,3,6,…为
解得
(2)
16. 解:(1)(2)证:
∴ 当(3)证:易算出当
由已知条件易知
(2)当
所以
等差、等比数列的综合应用
一. 教学内容:等差、等比数列的综合应用
二、教学目标:
综合运用等差、等比数列的定义式、通项公式、性质及前n项求和公式解决相关问题.
三、知识要点:
(一)等差数列
1. 等差数列的前
2. 等差数列的前
3.
5. 对等差数列前n项和的最值问题有两种方法:
(1)利用
当
(二)等比数列
1、等比数列的前n项和公式:
∴当
当q=1时,
2、
②当q≠-1或k为奇数时,
3、等比数列的性质:若m n=p k,则
【典型例题
例1. 在等差数列{
解:由等差中项公式:
=(
解:(用错项相消法)
①-②
当
∴
即:
∴即:
例4. 设首项为正数的等比数列,它的前
解:由题意
代入(1),
∴
∴
∴
∴此数列为
例5. 求集合M={m|m=2n-1,n∈N*,且m<60=的元素个数及这些元素的和。
∴满足不等式n<
答案:集合M中一共有30个元素,其和为900。
【模拟试题
1. 已知等比数列的公比是2,且前四项的和为1,那么前八项的和为 ( )
A. 15 B. 17 C. 19 D. 21
2. 已知数列{an=3n-2,在数列{an}中取ak2,akn ,… 成等比数列,若k1=2,k2=6,则k4的值 ( )
A. 86 B. 54 C. 160 D. 256
3. 数列A. 750 B. 610 C. 510 D. 505
4.
A. 5 B. 6 C. 7 D. 8
5. 若一个等差数列前3项的和为34,最后3项的和为146,且所有项的和为390,
则这个数列有 ( )
A. 13项 B. 12项 C. 11项 D. 10项
6. 数列
A.
9. 设
(1)问数列
∴
即当n=8或n=9时,
解法2:由已知解得
∴
又因为
数列的基本概念与等差数列
一. 教学内容:数列的基本概念与等差数列
二. 教学目标:
1. 理解数列及其有关概念,了解数列和函数之间的关系。
2. 了解数列的通项公式,并会用通项公式写出数列的任意一项。
3. 对于比较简单的数列,会根据其前几项写出它的通项公式。
4. 明确等差数列的定义,掌握等差数列的通项公式。
5. 熟练掌握等差数列的通项公式和前n项和公式。
6. 了解等差数列的一些性质,并会用它们解决一些相关问题。
三. 本周知识要点:
4,5,6,7,8,9,10. ①
1,
1,0.1,0.01,0.001,0.0001,…. ③
1,1.4,1.41,1.414,…. ④
-1,1,-1,1,-1,1,…. ⑤
2,2,2,2,2,…. ⑥
观察这些例子,看它们有何共同特点?
(一)数列的基本概念
1. 数列的定义:按一定次序排列的一列数叫做数列。
2. 数列的项:数列中的每一个数都叫做这个数列的项。各项依次叫做这个数列的第1项(或首项),第2项,…,第n 项,…。
3. 数列的一般形式:
⑵一个数列的通项公式有时是不唯一的,如数列:1,0,1,0,1,0,…,它的通项公式可以是
⑶数列通项公式的作用:①求数列中任意一项;②检验某数是否是该数列中的一项。
从映射、函数的观点来看,数列也可以看作是一个定义域为正整数集N*(或它的有限子集{1,2,3,…,n})的函数,当自变量从小到大依次取值时对应的一列函数值,数列的通项公式就是相应函数的解析式。
对于函数,我们可以根据其函数解析式画出其对应图象,看来,数列也可根据其通项公式画出其对应图象,下面同学们练习画数列①,②的图象,并总结其特点。
5. 数列的图像都是一群孤立的点。
6. 数列有三种表示形式:列举法,通项公式法和图象法。
7. 有穷数列:项数有限的数列。例如,数列①是有穷数列。
8. 无穷数列:项数无限的数列。
(二)等差数列
1. 等差数列:一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,这个数列就叫做等差数列,这个常数就叫做等差数列的公差(常用字母“d”表示)。
⑴公差d一定是由后项减前项所得,而不能用前项减后项来求;
⑵对于数列{
2. 等差数列的通项公式:
3. 等差中项:如果a,A,b成等差数列,那么A叫做 a与b的等差中项。
如数列:1,3,5,7,9,11,13…中
5是3和7的等差中项,1和9的等差中项。
9是7和11的等差中项,5和13的等差中项。
看来,4. 性质:在等差数列中,若m n=p q,则,
但通常 ①由
5. 等差数列的前
公式二又可化成式子:若
【典型例题
例1. 根据下面数列
解:(1)
例2. 写出下面数列的一个通项公式,使它的前4项分别是下列各数:
(1)1,3,5,7;
(2)
解:
(1)项1=2×1-1 3=2×2-1 5=2×3-1 7=2×4-1
↓ ↓ ↓ ↓
序号 1 2 3 4
即这个数列的前4项都是序号的2倍减去1,
∴它的一个通项公式是: (2)序号:1 2 3 4
↓ ↓ ↓ ↓
项分母:2=1 1 3=2 1 4=3 1 5=4 1
↓ ↓ ↓ ↓
项分子: 22-1 32-1 42-1 52-1
即这个数列的前4项的分母都是序号加上1,分子都是分母的平方减去1,∴它的一个通项公式是:
这个数列的前4项的绝对值都等于序号与序号加1的积的倒数,且奇数项为负,偶数项为正,所以它的一个通项公式是: 例3. ⑴求等差数列8,5,2…的第20项
⑵ -401是不是等差数列-5,-9,-13…的项?如果是,是第几项?
n=20,得⑵由得数列通项公式为:
由题意可知,本题是要回答是否存在正整数n,使得
例4. 在等差数列
解法一:∵
小结:第二通项公式 【模拟试题】
1、根据下面数列的前几项的值,写出数列的一个通项公式:
(1)3, 5, 9, 17, 33,……;
(2)
4、在等差数列
(2)
(4)将数列变形为1+0, 2+1, 3+0, 4+1, 5+0, 6+1, 7+0, 8+1, ……,
∴
2、(1)解:根据题意可知:
∴该数列的通项公式为:
∴
∴
(3)解:根据题意可得:<3" >
∴此数列通项公式为:
令-
因为-
3、解:(1)由题意得:
(2)解法一:由题意可得:
∴该数列的通项公式为:
4、解:由题意可知
解之得
或由题意可得:
可求得d=3,再由
数列、等差数列
一. 教学内容:
2.1 数列
2.2 等差数列
二. 教学目的:
1. 了解数列的概念,体会数列是一种特殊函数,能根据数列的前几项写出简单数列的通项公式。
2. 类比函数理解数列的几种表示方法(列表、图象、通项公式等),能根据项数多少、数列的性质对数列分类。
3. 掌握等差数列的概念、等差中项的概念,会根据定义判定数列是否是等差数列。
4. 掌握等差数列的通项公式及推导方法,会类比直线、一次函数等有关知识研究等差数列的性质,能熟练运用通项公式求有关的量:a1,d,n,an。
5. 掌握等差数列的前n项和公式及推导方法.当al,d,n,an,Sn中已知三个量时,能熟练运用通项公式、前n项和公式求另两个量。灵活运用公式解决与等差数列有关的综合问题。能构建等差数列模型解决实际问题。
三. 教学重点、难点:
重点:数列的概念、数列的通项公式;等差数列的通项公式和前n项和公式。
难点:等差数列的通项公式和前n项和公式的推导以及它们的综合运用。
四. 知识分析:
(一)数列
1. 数列的定义:按照一定次序排列的一列数叫数列,数列中每一个数叫这个数列的项,第n项记作an,叫做数列的通项,我们常把一般形式的数列简记作{an}。
2. 数列是特殊函数
数列可以看成以正整数集N+(或它的有限子集{1,2,3,…,n})为定义域的函数。an=f(n),当自变量按照从小到大依次取值时,所对应的一列函数值。
3. 通项公式:如果数列{an}的第n项与项数n之间的函数关系,可以用一个公式an=f(n)来表示,那么就把这个公式叫这个数列的通项公式。
通项公式可以看成数列的函数解析式。
4. 数列的分类:
(1)按项数有限还是无限来分:有穷数列和无穷数列;
(2)按照项与项之间的大小关系来分:递增数列、递减数列、摆动数列、常数列。
5. 前面学习过数集,如果把数集中的元素按一定顺序排成一列,就是数列。但数列和数集有较大区别:数集中的元素是无序的,也是互异的;而数列中的元素却是有序的,而且是可以重复出现的。
6. 根据所给出的数列的前几项,写出符合要求的一个通项公式,主要方法是:
①要观察给出的若干数中的“不变”的内容,注意研究an与n的关系。
②多角度思考,全方位观察,广泛联想,将原数列作出适当的转化变形后,化为基本数列或特殊数列,常用技巧是:分解条件,寻找规律。
7. 如何利用数列与函数的关系来解题?
一方面,数列是一个特殊的函数,因此在解决数列问题时,要善于利用函数的知识、函数的观点、函数的思想方法来解题,即用共性来解决特殊问题。如由数列是定义在N*和它的子集{1,2,3,…,n}的函数可知an是n的函数,即an=f(n)。因此当{an}通项公式的一端的某个“n”用某个数或某个式或某个记号代替后,则两端的所有的“n”必须用同一个代替,特别地有
8. 如果已知数列{an}的第一项(或前几项),且从第二项(或某一项)开始的任一项an与它的前一项an-1(或前几项)间的关系可以用一个式子来表示,那么这个公式叫做这个数列的递推公式。
9. 若数列{an}的前n项和记为Sn,即
10. 通项公式和递推公式的区别在于:通项公式直接反映an和n之间的关系,即an是n的函数,知道任意一个具体的n值,通过通项公式就可以求出该项的值an;而递推公式则是间接反映数列的式子,它是数列任意两个(或多个)相邻项之间的推导关系,不能由n直接得出an
11. 用递推公式给出一个数列,必须给出①“基础”?D?D数列{an}的第1项或前几项;②递推关系?D?D数列{an}的任一项an与它的前一项an-1(或前几项)之间的关系,并且这个关系可以用一个公式来表示。
如果两个条件缺一个,数列就不能确定。例如,已知数列{an}的al=1,a2=2,这个数列就不能确定。因为有的说an=n;有的说
若a1适合
(二)等差数列
1. 等差数列的定义:一般地,如果一个数列{an}从第二项起,每一项与它的前一项的差都等于同一个常数,用式子可表示为
2. 等差数列的单调性:等差数列的公差d>0时,数列为递增数列;d<0时,数列为递减数列;d=0时,数列为常数列。
3. 等差数列的通项公式
4. 要证明数列{an}为等差数列,只要证明:当
5. 对等差数列{an}而言:
(l)公差是从第二项起,每一项减去它前一项的差(同一常数),即
(3)
由此可利用共线的方法解决有关等差数列问题。
(4)对任意的m,n∈N*,有
(5)公式中含四个量a1,an,d,n,已知任意三个,可求第四个量。
6. 如果三个数a,A,b组成等差数列,那么A叫做a与b的等差中项。
7. 等差数列的判定方法
(1)
(3)
(5)
(7)数列
(8)下标成等差数列且公差为m的项
(9)若
(11)
(2)若有三个数成等差数列,则一般设为
2. 若数列{an}的前n项和公式为
(2)当A≠0,即d≠0时,(*)式是n的二次函数,即(n,Sn)在
(3)在求等差数列的和Sn时,如已知al、an、n,可用公式
6 . 若在等差数列{an}中,a1>0,d<0,则Sn存在最大值;若在等差数列{an}中,a1<0,d>0,则Sn存在最小值。
7. 若
(四)与和有关的等差数列的性质:
1. 若项数为2n
若项数为
4. 若
【典型例题】
例1. 写出下面数列的一个通项公式,使它的前4项分别是下列各数:
解析:若要根据给出的前 4 项写出数列的通项公式,首先要细心观察四个数变化的规律,为了便于发现规律应注意两点:
第一是将个别破坏规律的项还原,如(l)中首先观察发现第一个数1应写成分数
点评:
1. 求数列的通项公式时,一般通过分解?D?D探索?D?D综合的方法进行归纳。要注意观察数列中的各项通过分解后哪些部分是不变的,哪些部分是变化的,变化的部分随其序号的变化情况如何,归纳时要重视从整体上把握数列的构成规律,写出通项公式。
2. 为了方便,掌握下面一些简单的常用数列的通项公式是有好处的:
证明:
整理得
∴从第1项到第9项递增,从第10项起递减。
点评:数列是特殊函数,可用研究函数的方法研究数列相应问题(如本题数列的增减性)
例3. 已知数列
解法一:设数列
由已知得360docimg_501_
解之得360docimg_502_
360docimg_503_
360docimg_504_
则由题设,得360docimg_505_
故所求四数分别为2,5,8,11或11,8,5,2
解法二:设这四个数分别为360docimg_506_
360docimg_507_
所以所求四数分别为2,5,8,11或11,8,5,2
点评:本题巧设未知数,减少了未知量,简化了运算。一般地,三个数成等差数列,且它们的和已知时,可设为a-d,a,a d。而四个数可设为a-3d,a-d,a d,a 3d(公差为2d)。
例5. (2005年北京市模拟题)已知a,b,c成等差数列,那么a2(b+c),b2(c a),c2(a b)是否构成等差数列?
证明:∵a,b,c成等差数列 ∴360docimg_508_
360docimg_509_
即360docimg_510_。
(2)360docimg_511_
整理得360docimg_512_
解之得n=12或360docimg_513_
解之得n=4
又由360docimg_514_
即得360docimg_515_
360docimg_516_
360docimg_517_
解法二:由360docimg_518_
得360docimg_519_
360docimg_520_
点评:a1,d,n称为等差数列的三个基本量,an和Sn都可以用这三个基本量来表示,五个量 a1,d,n,an,Sn中可知三求二,即等差数列的通项公式及前n项和公式中“知三求二”的问题,一般是通过通项公式和前n项和公式联立方程(组)求解。这种方法是解决数列运算的基本方法,在具体求解过程中应注意已知与未知的联系及整体思想的运用。
例7. 已知数列360docimg_521_的前n项和360docimg_522_,求数列360docimg_523_的前n项和360docimg_524_
∵n=1也适合上式
∴数列360docimg_525_
由360docimg_526_时
360docimg_527_
(2)当360docimg_528_
故360docimg_529_
点评:由an与Sn的关系求通项公式是一类重要题型,要注意分类讨论的必要性。
例8. (2005年西安市统考题)一个等差数列的前10项之和为100,前100项之和为10,求前110项之和。
解法一:设等差数列360docimg_530_的公差为d,前n项和360docimg_531_
则360docimg_532_
由已知得360docimg_533_
①×10-②整理得360docimg_534_
360docimg_535_
360docimg_536_
故此数列的前110项之和为-110
解法二:设360docimg_537_
360docimg_538_
360docimg_539_
解法三:设等差数列的首项为360docimg_540_,公差为d
则360docimg_541_
①-②得
360docimg_542_
360docimg_543_成等差数列,设其公差为D。前10项的和360docimg_544_
360docimg_545_
又360docimg_546_
点评:本例解法较多,望同学们认真分析每种解法的思想实质,达到开阔思想探索研究,寻求简捷解法的目的。解法一是基本方法,不容忽视,解法二属函数观点,高瞻远瞩,解法三运用整体思想,解法四则利用性质,简捷明快,解法五利用了等差数列的性质。
【模拟试题】
1. 数列360docimg_547_的通项公式360docimg_548_,作为函数,它的定义域是( )
A. 正整数集N*
B. 自然数集N
C. 正整数集N*或N*的任一子集
D. 正整数集N*,或其有限子集{1,2,…,n}
2. 下列说法中,正确的是( )
A. 数列1,3,5,7可表示为{1,3,5,7}
B. 数列1,0,-1,-2与数列-2,-1,0,1是相同的数列
C. 数列360docimg_549_)两数之间插入n个数,使它们与a,b组成等差数列,则该数列的公差为( )
A.360docimg_550_C.360docimg_551_
4. 在数列{360docimg_552_,则360docimg_553_都是等差数列,且360docimg_554_,则360docimg_555_+360docimg_556_,则此数列前20项的和等于( )
A. 160 B. 180 C. 200 D. 220
7. (2004年福建文)设Sn是等差数列360docimg_557_的前n项和,若360docimg_558_( )
A. 1 B. -1 C. 2 D.360docimg_559_
8. (2004年重庆卷)若360docimg_560_是等差数列,首项360docimg_561_成立的最大自然数n是( )
A. 4005 B. 4006 C. 4007 D. 4008
9. (2005年吉林省实验中学第一次检测)在等差数列360docimg_562_中,360docimg_563_,则360docimg_564_等于__________。
11. 等差数列360docimg_565___________。
12. 在数列360docimg_566_中,已知360docimg_567_,那么使其前n项和360docimg_568_,两个数列:360docimg_569_都是等差数列,求360docimg_570_
其中每行、每列都是等差数列,360docimg_571_的计算公式。
15. 设360docimg_572_为等差数列,360docimg_573_为数列360docimg_574_的前n项和,已知360docimg_575_的前n项和,求360docimg_576_。
(1)求通项360docimg_577_12. 12
13. 解:设两个等差数列的公差分别为360docimg_578_
解得360docimg_579_
14. 解:(1)360docimg_580_
第二行是首项为7,公差为5的等差数列
360docimg_581_,公差为360docimg_582_
15. 解:设等差数列360docimg_583_的公差为d,则
360docimg_584_
解得360docimg_585_
360docimg_586_
360docimg_587_
360docimg_588_
16. 解:(1)360docimg_589_
360docimg_590_
360docimg_591_
360docimg_592_
360docimg_593_
故360docimg_594_
数列通项与数列求和
一. 教学内容:数列通项与数列求和
二. 教学要求:
n求an时,用公式an=Sn-1要注意a1应由an+1-f(n),f(an+1=q,分别用累加法、累乘法、迭代法(或换元法).
2、数列的前n项和
(1)数列求和的常用方法有:公式法、分组求和法、错位相减法、裂项相消法、倒序求和法等。
求数列的前n项和,一般有下列几种方法:
(2)等差数列的前n= = .
(3)等比数列的前q=1时,Sq≠1时,Sn的数列,求前n项和时,应注意讨论n的奇偶性。
③倒序相加和错位相减法是课本中分别推导等差、等比数列前360docimg_595_,360docimg_596_是等比数列,并求360docimg_597_,∴360docimg_598_
假设存在某个360docimg_599_,则可以推出与360docimg_600_矛盾。
∴360docimg_601_。
例2. 在数列360docimg_602_=n?360docimg_603_的表达式。
360docimg_604_的前n项和Sn的公式,求360docimg_605_
例4. 设数列解:设360docimg_606_
例5. (天津文20)在数列360docimg_607_中,360docimg_608_,360docimg_609_.
(I)证明数列360docimg_610_是等比数列;
(II)求数列360docimg_611_的前360docimg_612_项和360docimg_613_,得
360docimg_614_.
又360docimg_615_是首项为360docimg_616_,且公比为360docimg_617_,于是数列360docimg_618_的通项公式为
360docimg_619_.
所以数列360docimg_620_的前360docimg_621_项和360docimg_622_.
例6. 已知数列:1,360docimg_623_,360docimg_624_,求它的前n项的和Sn.
解:∵360docimg_625_+360docimg_626_+……+360docimg_627_
=360docimg_628_∴an=2-360docimg_629_
则原数列可以表示为:
(2-1),360docimg_630_,360docimg_631_,…前n=(2-1)+360docimg_632_+…+=2360docimg_633_
=2360docimg_634_=2n-2=360docimg_635_+2n-2
例7. 已知数列{n项和Sn2-9(1)求证:{ n的最小值及相应的n项和为Tn,求T解:(1)a1=S1=-8
an=Sn-1=2
∴ n-10 an=2
∴ {n=n2-9n-360docimg_636_)2-360docimg_637_
∴当n=4或n有最小值-20.
(3)n-10 ∴ | an |=| 2an≥0360docimg_638_n≤4时,|n
Tn=360docimg_639_,当n=-a2-a4+a6+…+=(a1+a2+…+an)-(a1+a2+a3+a4)=S=n2-9n2-9n=360docimg_640_
数列360docimg_641_项和。
360docimg_642_,求前360docimg_643_项和。
360docimg_644_
360docimg_645_
例11. 已知函数f(x)=(x-1)2,数列{an}是公差为d的等差数列,数列{bn}是公比为q的等比数列(q≠1),若a1=f(d-1),a3=f(d+1),b1=f(q-1),b3=f(q+1),
(1)求数列{an},{bn}的通项公式;
(2)设数列{cn}对任意的自然数n均有:360docimg_646_,求数列{cn}的前n项和Sn.
解:(1) d-2)2,d2,a3-a1=2d2-(d-2)2=2d,解之得a1=0,n-1)
又b1=(q-2)2,q2,b3=b1q2
即q2=(q-2)2q=3
∴b1=1,n-1
(2)360docimg_647_
n
=4(1×30+2×31+3×32+…+ n-1)
设n×3360docimg_648_1×31+2×32+3×33+…+n×3360docimg_649_1+3+32+33+…+3n×3360docimg_650_n?n
360docimg_651_
∴Sn=2n?3n+1
【模拟试题
1. 数列360docimg_652_=
3. 数列{360docimg_653_的前20项和为
4. 已知数列360docimg_654_的通项公式为
5. 设360docimg_655_则360docimg_656_的值为
6. 求数列1,360docimg_657_的前360docimg_658_项和。
7. 数列360docimg_659_的前360docimg_660_项和360docimg_661_项和360docimg_662____________
9. 数列360docimg_663_的前360docimg_664_项和为
10. 求和:360docimg_665_项和的公式的方法,可求得
360docimg_666_360docimg_667_,360docimg_668_,求:13. 已知数列{an}是公差为d的等差数列,数列{bn}是公比为q(q∈R且q≠1)的等比数列,若函数f (x)=(x-1)2,且a1 = f (d-1),a3 = f (d 1),b1 = f (q 1),b3 = f (q-1),求数列{ a n }和{ b n }的通项公式。
360docimg_669_
【试题答案】
1.360docimg_670_,
360docimg_671_
7.360docimg_672_
8. 1
9.360docimg_673_
10.
360docimg_674_
11.360docimg_675_
360docimg_676_
360docimg_677_
等比数列、数列求和
一. 教学内容:等比数列、数列求和
二. 重点、难点:
1. 理解等比数列的有关概念;掌握等比数列的通项公式和前360docimg_678_项和公式,并能运用这些知识解决一些简单的实际问题。
2. 通过观察数列通项公式的特点选择合适的方法,求数列的前360docimg_679_项和。
【典型例题
[例1] 在等比数列360docimg_680_,360docimg_681_,求360docimg_682_和360docimg_683_是等比数列,故360docimg_684_,结合360docimg_685_,可知360docimg_686_的两根,解方程,得360docimg_687_
故360docimg_688_,360docimg_689_或360docimg_690_时,360docimg_691_,得360docimg_692_,故360docimg_693_360docimg_694_
当360docimg_695_时,360docimg_696_
综上所述,360docimg_697_或360docimg_698_
[例2] 已知数列360docimg_699_,360docimg_700_,360docimg_701_
解:设360docimg_702_成等比数列
∴360docimg_703_
∵360docimg_704_
∴360docimg_705_
360docimg_706_为等差数列,360docimg_707_,360docimg_708_。
解:由360docimg_709_为等比数列
∴360docimg_710_
由已知360docimg_711_∵360docimg_712_∴360docimg_713_知360docimg_714_
360docimg_715_知
360docimg_716_或360docimg_717_或360docimg_718_
[例4] 设等比数列360docimg_719_,360docimg_720_)
解:方法一:设公比为360docimg_721_化简得360docimg_722_解得360docimg_723_
设数列360docimg_724_前360docimg_725_项和为360docimg_726_,则
360docimg_727_360docimg_728_360docimg_729_
可见,当360docimg_730_时,<4" >360docimg_731_最大
而360docimg_732_,
故360docimg_733_的前5项和最大
方法二:接前,360docimg_734_于是360docimg_735_
∴ 数列<9" >360docimg_736_是以360docimg_737_为首项,以360docimg_738_,得360docimg_739_
由于360docimg_740_∴360docimg_741_的前5项和最大
[例5] 求数列的前360docimg_742_项和:360docimg_743_
360docimg_744_时,360docimg_745_时,
360docimg_746_
[例6] 在数列360docimg_747_,求数列360docimg_748_项的和。
解:∵360docimg_749_
∴ 数列360docimg_750_项和
360docimg_751_
360docimg_752_的值。
解:设360docimg_753_①
将①式右边反序得
360docimg_754_
① ②得360docimg_755_
[例8] 已知数列360docimg_756_的表达式;
(2)如果360docimg_757_,求360docimg_758_项和360docimg_759_
解:
(1)360docimg_760_,当360docimg_761_
∴360docimg_762_
因而360docimg_763_
∴360docimg_764_①
则360docimg_765_360docimg_766_
360docimg_767_又1 3 5 …360docimg_768_
[例9] 已知数列360docimg_769_项和为360docimg_770_,且满足360docimg_771_),360docimg_772_是等差数列;
(2)求360docimg_773_时,求证:360docimg_774_
解:
(1)证明:∵360docimg_775_
360docimg_776_
又360docimg_777_∴360docimg_778_
∴ 当360docimg_779_[或360docimg_780_]
当360docimg_781_时,360docimg_782_
∴360docimg_783_
(3)证明:由(2)知,
360docimg_784_
360docimg_785_中,首项360docimg_786_等于( )
A. 33 B. 72 C. 84 D. 189
2. 若等比数列360docimg_787_的公比360docimg_788_项和为360docimg_789_,则360docimg_790_与360docimg_791_的大小关系是( )
A.360docimg_792_C.360docimg_793_满足360docimg_794_(360docimg_795_),则当360docimg_796_时,360docimg_797_B.360docimg_798_C.360docimg_799_中,若360docimg_800_B.360docimg_801_D.360docimg_802_(360docimg_803_)的结果是( )
A.360docimg_804_C.360docimg_805_D.360docimg_806_
6. 数列360docimg_807_项和为360docimg_808_,则360docimg_809_等于( )
A. 1003 B.360docimg_810_C. 2006 D.360docimg_811_等于( )
A.360docimg_812_
B.360docimg_813_
D.360docimg_814_,第三年的增长率为360docimg_815_,则下列关系正确的是( )
A.360docimg_816_C.360docimg_817_
二. 解答题:
1. 等比数列360docimg_818_项中,数值最大的一项是54,若该数列的前360docimg_819_,求:
(1)前100项之和360docimg_820_。
2. 已知数列1,360docimg_821_,360docimg_822_(360docimg_823_项和。
3. 已知360docimg_824_
(1)当360docimg_825_的前360docimg_826_项和360docimg_827_;
(2)求360docimg_828_
4. 设数列360docimg_829_的等差数列,求和:360docimg_830_
360docimg_831_
360docimg_832_
【试题答案】
一.
1. C
解析:∵360docimg_833_,360docimg_834_或2. A
解析:由等比数列通项公式和前360docimg_835_项和公式得
360docimg_836_
360docimg_837_
360docimg_838_又360docimg_839_, 即3. C
解析:由已知360docimg_840_
得到360docimg_841_,360docimg_842_由此猜想出4. D
解析:由360docimg_843_),当360docimg_844_时,360docimg_845_不适合,所以360docimg_846_
5. B
解析:∵360docimg_847_
360docimg_848_
6. A
解析:360docimg_849_(共1003个)=1003
7. D
解析:原式360docimg_850_
8. B
解析:设平均增长率为360docimg_851_,则第三年产量为360docimg_852_,所以应该有360docimg_853_
即360docimg_854_
二.
1. 解:设公比为360docimg_855_
∴360docimg_856_(∵360docimg_857_②
360docimg_858_③
由①②③解得360docimg_859_,则
(1)前100项之和360docimg_860_
(2)通项公式为360docimg_861_
2. 解:由题意可知,360docimg_862_的通项是等差数列360docimg_863_的通项与等比数列360docimg_864_的通项之积,设①-②得当360docimg_865_
∴360docimg_866_
当360docimg_867_时,360docimg_868_
3. 解析:
(1)当360docimg_869_,这时数列360docimg_870_项和360docimg_871_①
①式两边同乘以360docimg_872_,得360docimg_873_
若360docimg_874_
360docimg_875_
若360docimg_876_时,360docimg_877_
则360docimg_878_
当360docimg_879_
360docimg_880_此时,360docimg_881_
若360docimg_882_,360docimg_883_
若360docimg_884_,360docimg_885_
4. 解析:∵ ∴ ∴ 又360docimg_886_